Platone, nel raccontare e descrivere l’Atlantide nei dialoghi Timeo e Crizia, utilizza le scienze della geografia e della geometria, in questo articolo prendiamo in considerazione quest’ultima, partendo dal sistema di misurazione in uso ai suoi tempi, l’antico stadio greco, che convertiamo in metri.
Poiché ancora oggi non c’è uniformità di vedute circa le misure esatte da accordare a questo sistema, noi prenderemo una media standard, tenendo comunque ben presente che lo stadio greco corrisponde a sei volte la misura del pletro:
- 1 stadio = 178 metri circa
- 1 pletro = 29,67 metri circa
- 1 piede = 30 centimetri circa
La pianura di Atlantide
Cominciamo allora dalla descrizione che Platone ci fornisce della pianura di Atlantide.
Si diceva primamente che tutto il luogo fosse molto alto e scosceso dalla parte del mare, e tutt’intorno una pianura circondasse la città, e questa pianura, cinta in giro da monti discendenti fino al mare, fosse liscia e uniforme e tutta oblunga, di tremila stadi da una parte e di duemila dal mare fino al centro
Crizia 118a
Era esso un quadrangolo per la maggior parte retto e oblungo, e dove veniva meno, lo rendeva diritto una fossa scavata all’intorno
Crizia 118c
La pianura era dunque un rettangolo di duemila stadi per tremila stadi, ovvero 356 chilometri per 534 chilometri, e, come se Platone a questo punto avesse temuto di non essere creduto, ci invita a calcolare ancora, non una, ma ben due volte, cominciando dalla fossa scavata intorno alla pianura.
Però bisogna dire quel che abbiamo udito. [La fossa] era stata scavata alla profondità di un pletro con la larghezza d’uno stadio in ogni punto, ed essendo condotta per tutta la pianura ne conseguiva che avesse la lunghezza di diecimila stadi
Crizia 118c
Diecimila stadi sono 1780 Km, ovvero il perimetro della pianura stessa (356+356+534+534), e prosegue dicendo:
In quanto alla moltitudine degli uomini che nel piano erano utili alla guerra, era stato stabilito che ogni divisione presentasse un capo, e la grandezza d’ogni divisione era di cento stadi, e tutte le divisioni erano sessantamila
Crizia 118e
Dobbiamo calcolare ancora. La terra venne divisa in più lotti, o divisioni, di 100 stadi; quindi per arrivare a calcolarne l’area, tenendo conto che 10 stadi equivalgono a 1,78 Km, otterremo
100 stadi = 1,78 Km x 1,78 Km = 3,1684 Km². 3,1684 Km²
moltiplicati per i 60000 lotti di terreno danno un risultato di 190.104 Km², che equivalgono all’area della pianura:
356 Km x 534 Km = 190.104 Km²
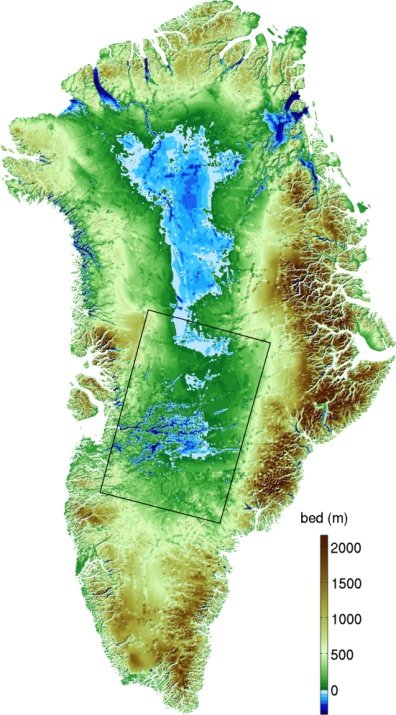
Platone parla esplicitamente di una pianura “oblunga”, ma vista l’impossibilità, per il momento di poter osservare nel dettaglio al di sotto dei ghiacci della Groenlandia, la ricostruiremo ad angoli retti:
Ricostruzione della pianura di Atlantide
Ora siamo pronti a sovrapporre in scala, la pianura così realizzata come indicato da Platone, con la ricostruzione geomorfologica della Groenlandia realizzata grazie a sorvoli aerei e satellitari dotati di GeoRadar.
La Groenlandia con e senza la sua calotta di ghiaccio, con inserita in scala la fossa quadrangolare.
La città di Atlantide
Passiamo ora alla descrizione della città di Atlantide:
[Poseidone] per ben fortificare il colle, in cui quella abitava, lo spezzò d’ogni intorno, e vi pose alternativamente cinte minori e maggiori di mare e di terra, due di terra e tre di mare, che quasi descrisse in cerchio dal centro dell’isola, ponendole ad egual distanza per ogni parte, cosicché non vi fosse accesso per gli uomini: perché a quel tempo non v’erano ancora navi né navigazioni
Crizia 113d
Poseidone, che era un dio e poteva quindi realizzare tutto ciò che gli uomini non possono fare, individuò quella che potremmo chiamare una collina primordiale non lontana dal mare e per difenderla vi creò attorno, nella pianura circostante, delle cinte alternate di terra e di mare.
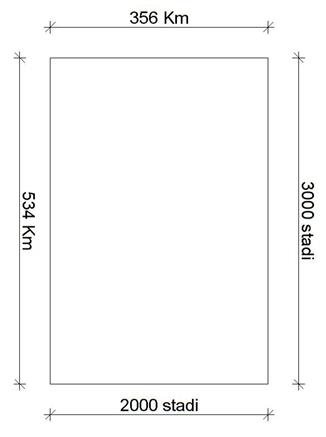
Dopodiché, prosegue il racconto, avendo avuto discendenza mortale, lasciò ai suoi figli umani il compito di proseguire i lavori. Questi, senza perdere tempo, realizzarono un canale di collegamento tra il mare a l’anello esterno della città largo 89,00 metri (3 pletri), lungo 8,9 chilometri (50 stadi) e profondo 30 metri (100 piedi) (Crizia 115d).
Il racconto prosegue con la descrizione precisa delle dimensioni degli anelli di terra e di mare:
Ma la più grande delle cinte, con la quale comunicava il mare, era larga tre stadi, e quella successiva di terra era uguale ad essa: delle due cinte seguenti, la marittima era larga due stadi, la terrestre era uguale alla marittima precedente: infine d’uno stadio era quella che circondava l’isola nel mezzo. L’isola, in cui stava la reggia, aveva il diametro di cinque stadi
Crizia 115e
A questo punto la città, o meglio, il terreno modellato prima da un dio e poi dagli uomini, è completato e pronto per essere edificato; e anche noi, grazie all’utilizzo di un programma Cad, possiamo ricostruire l’intera area così come descritta da Platone; di forma circolare, con anelli di terra e mare alternati e un diametro totale di 4 chilometri e 806 metri.
Osservando attentamente la figura riportata di seguito, possiamo anche intuire cosa si celi in realtà dietro la “collina spezzata da Poseidone”, non un’invenzione di Platone per descrivere la sua città ideale, ma una formazione geologica di tipo astronomico.
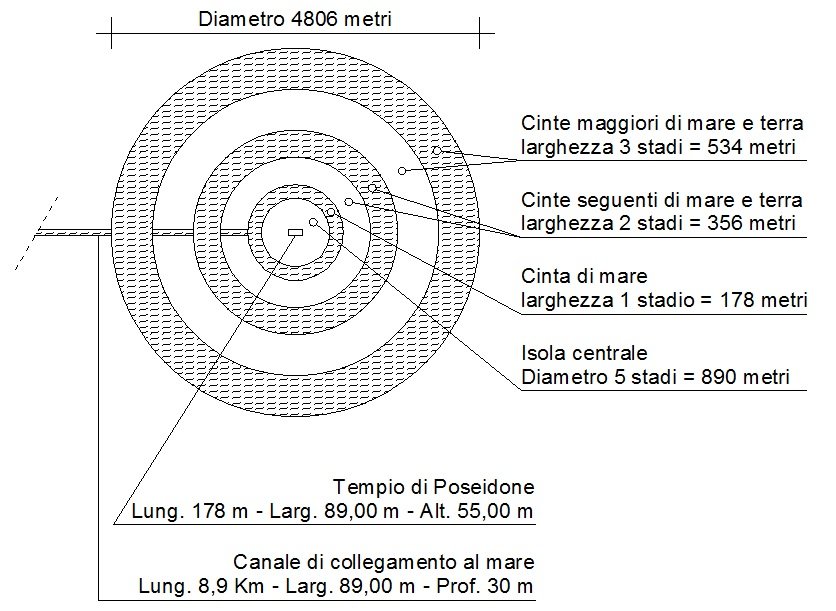
Ricostruzione della città di Atlantide
Il Tempio di Poseidone
Per concludere, il Tempio di Poseidone nell’isola centrale:
Il tempio di Poseidone era lungo uno stadio, largo tre pletri, d’altezza proporzionata a queste dimensioni, e con qualcosa di barbarico nell’aspetto
Crizia 116d
Platone colloca nell’isola centrale, il maestoso Tempio dedicato a Poseidone, invitandoci a calcolare l’altezza dell’edificio nello stesso modo in cui gli architetti del suo tempo progettavano e costruivano i grandiosi templi dedicati agli dei (ma vale anche per le cattedrali del medioevo come ad esempio Notre-Dame), fra cui anche il famoso Partenone di Atene, cioè utilizzando la sezione aurea, la quale si esprime con il numero 1,618.
Tempio di Poseidone: Lunghezza 178 metri, larghezza 89,00 metri, altezza 89,00/1,618 = 55,00 metri.
Ma c’è di più, poiché la lunghezza del Tempio è il doppio della sua larghezza, quindi due quadrati affiancati, potremmo anche ipotizzare che i costruttori avessero voluto includere nelle sue misure, lo sviluppo del rettangolo aureo partendo appunto da questi due quadrati di valore 1, aventi per lato la sequenza iniziale di ogni forma vivente, oggi conosciuta come successione di Fibonacci: 1, 1, 2, 3, 5, 8 e così via all’infinito.
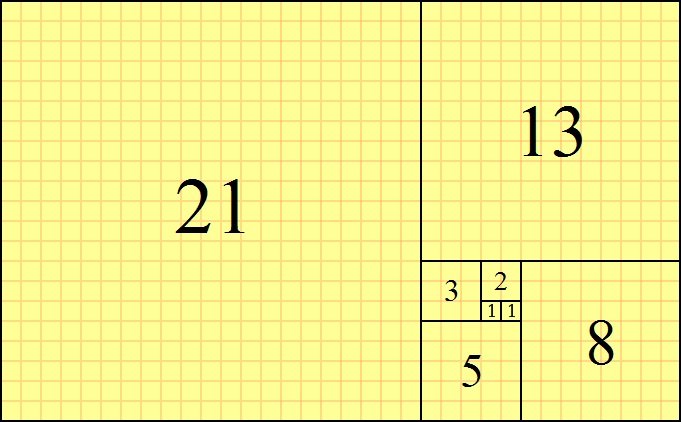
il Tempio di Poseidone (rettangolo 1 – 1) e la successione di Fibonacci.
Il tempio di Poseidone, edificato al centro della collina, era stato poi rivestito dentro e fuori con argento, oro, avorio e il misterioso oricalco. Successivamente era stato arredato con statue che sfioravano l’altezza del soffitto. Era, insomma, un edificio degno di un dio.