Tutti conosciamo, almeno per sentito dire il Numero Aureo (1,618) e il rettangolo omonimo, così chiamato perché i suoi lati sono tra loro in proporzione aurea1.
Guardando la figura si capisce facilmente con quale procedimento sia stato tracciato questo rettangolo.
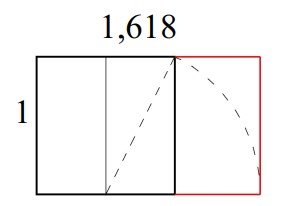
Rettangolo aureo
Partendo dal quadrato di lato 1 (nero) abbiamo aggiunto una parte (in rosso) ricavata ruotando la diagonale del semi-quadrato (linee tratteggiate).
Una delle particolarità più intriganti di un rettangolo aureo è costituita dal fatto che sottraendo al rettangolo aureo il quadrato (quello nero), rimane il rettangolo (quello rosso) il quale, a sua volta è un rettangolo aureo.
Forse non tutti sanno che esiste anche il Numero Argenteo (2,414) e il suo relativo rettangolo omonimo, così chiamato perché i suoi lati sono tra loro in proporzione argentea2.
Ad un occhio un po’ allenato non sfuggirebbe che 2,414 è un numero composto da 1 + 1,414.
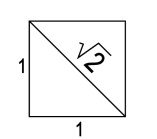
Diagonale del quadrato
Dove:
- 1 rappresenta l’unità,
- 1,414 è il valore numerico della Radice di 2 (√2).
La Radice di 2 (ovvero 1,414) è una importante costante matematica che è molto conosciuta in geometria in quanto rappresenta il valore della diagonale di un quadrato unitario, cioè con lato = 1.
Alla luce di queste cose, il Rettangolo Argenteo presenta le seguenti misure. Lato corto = 1 e lato e lato lungo = 2,414 in quanto composto da 1+1,414.
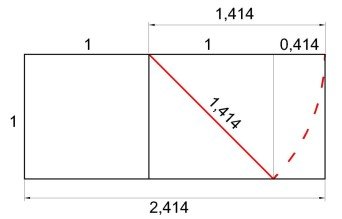
Rettangolo argenteo
In altre parole esso è uguale alla somma geometrica di un quadrato, più un rettangolo che abbia il suo lato lungo uguale a 1,414 cioè alla radice di 2.
Lato che si ottiene ruotando la diagonale del secondo quadrato (linee tratteggiate), come indicato nella figura a lato.
Come il suo omologo aureo, anche il Rettangolo Argenteo possiede una analoga particolarità intrigante. Infatti sottraendo ad esso i due quadrati, rimane (nella figura in fondo a destra) un piccolo rettangolo posizionato verticalmente il quale è, a propria volta, un rettangolo argenteo.
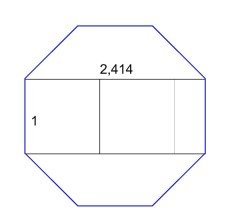
Ottagono argenteo
Un esempio di rettangolo argenteo lo possiamo trovare (in nuce) all’interno di una figura geometrica molto utilizzata specie nell’architettura rinascimentale: l’ottagono.
L’ottagono lo si trova molto spesso come figura di partenza per le cupole delle chiese (es. Cupola di Santa Maria del Fiore a Firenze di Brunelleschi) o Santa Maria di miracoli a Roma.
Un altro utilizzo della proporzione argentea, la possiamo trovare all’interno del foglio da stampa normato A3, dove, se il lato lungo vale 2, quello corto vale radice di 2.
A questo punto ci si potrebbe chiedere che posto possa occupare un simile rettangolo nella storia dell’architettura.
Un esempio che ho scovato di recente e che ha colpito la mia curiosità è il Mausoleo dell’imperatore Qin Shi Huang, scoperto nel 1974, che si trova nello Xi’an, nella provincia di Shaanxi e che è stato proclamato Patrimonio dell’Umanità.
Questo straordinario complesso funerario fu eretto nel 250 a.C. circa contiene una incredibile camera funeraria. Ecco come la descrive Wikipedia:
La camera funeraria di Qin Shi Huang (260 a.C.-210 a.C.), non ancora portata alla luce, sarebbe così profonda da attraversare tre livelli di falde acquifere, con pareti in bronzo e circondata da fiumi di cinabro, cioè solfuro di mercurio che, per la filosofia taoista, sarebbe un attivatore energetico per l’immortalità. Ad oggi, gli scavi archeologici hanno portato alla luce diversi complessi secondari tra cui quello ospitante il famoso esercito di terracotta.
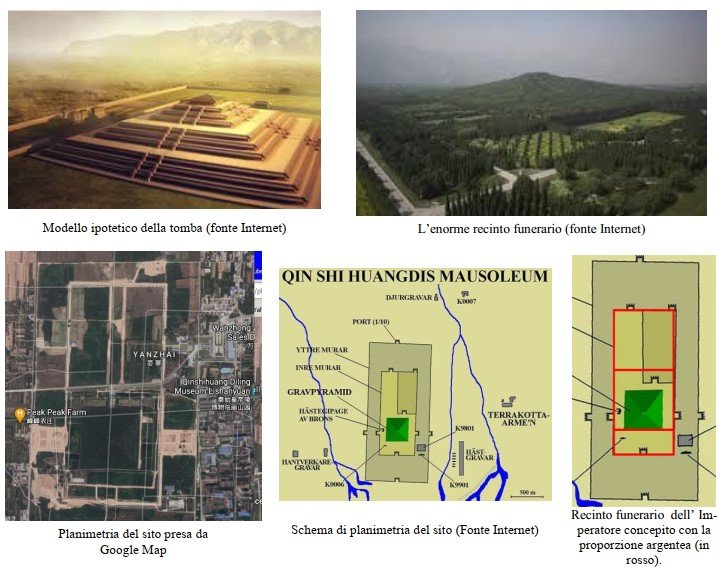
Da grande appassionato di architettura antica con particolare riferimento alle civiltà della Mezzaluna Fertile, del vicino Oriente e dell’Egitto, non posso che ammirare questo grande esempio di architettura funeraria.
Quello che continuo ad osservare che tutti i popoli antichi, quando decidevano di fare delle opere architettoniche di pregio e di grande qualità e che, a mio modesto avviso, dovevano trasportare nei secoli un messaggio, “stranamente” usavano tutti (in ogni epoca e sotto ogni cielo) le stesse norme proporzionali, segno che queste sono insite nell’uomo fin dagli albori della civiltà. I rettangolo argenteo è una di queste…
1 – Rivediamo, per chi non ricordasse, la definizione di proporzione aurea: Due quantità tra loro disuguali sono in rapporto aureo tra loro, quando la più grande è “medio proporzionale” tra la più piccola e la somma delle due. Se chiamiamo A la quantità piccola, B quella grande, il concetto di proporzione aurea, si può riassumere con la proporzione: A : B = B : A+B.
2 – Rivediamo, per chi non conoscesse, la definizione di proporzione argentea: Due quantità tra loro disuguali sono in rapporto argenteo tra loro, quando la più grande è “medio proporzionale” tra la più piccola e la somma della minore e del doppio della maggiore. Se chiamiamo A la quantità piccola, B quella grande, il concetto di proporzione argentea, si può riassumere con la proporzione: A : B = B : A+2B.





